First Hardy–Littlewood conjecture

First Hardy–Littlewood conjecture

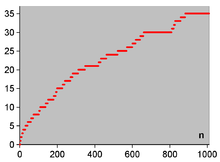Plot showing the number of twin primes less than a given n. The first Hardy–Littlewood conjecture predicts there are infinitely many of these.
Field	Number theory
Conjectured by	G. H. Hardy John Edensor Littlewood
Conjectured in	1923
Open problem	yes

In number theory, the first Hardy–Littlewood conjecture states the asymptotic formula for the number of prime k-tuples less than a given magnitude by generalizing the prime number theorem. It was first proposed by G. H. Hardy and John Edensor Littlewood in 1923.

Statement

Let $m_{1},m_{2},\ldots ,m_{k}$ be positive even integers such that the numbers of the sequence $P=(p,p+m_{1},p+m_{2},\ldots ,p+m_{k})$ do not form a complete residue class with respect to any prime and let $\pi _{P}(n)$ denote the number of primes $p$ less than $n$ st. $p+m_{1},p+m_{2},\ldots ,p+m_{k}$ are all prime. Then

$\pi _{P}(n)\sim C_{P}\int _{2}^{n}{\frac {dt}{\log ^{k+1}t}},$

where

$C_{P}=2^{k}\prod _{q{\text{ prime,}} \atop q\geq 3}{\frac {1-{\frac {w(q;m_{1},m_{2},\ldots ,m_{k})}{q}}}{\left(1-{\frac {1}{q}}\right)^{k+1}}}$

is a product over odd primes and $w(q;m_{1},m_{2},\ldots ,m_{k})$ denotes the number of distinct residues of $0,m_{1},m_{2},\ldots ,m_{k}$ modulo $q$.

The case $k=1$ and $m_{1}=2$ is related to the twin prime conjecture. Specifically if $\pi _{2}(n)$ denotes the number of twin primes less than n then

$\pi _{2}(n)\sim C_{2}\int _{2}^{n}{\frac {dt}{\log ^{2}t}},$

where

$C_{2}=2\prod _{\textstyle {q{\text{ prime,}} \atop q\geq 3}}\left(1-{\frac {1}{(q-1)^{2}}}\right)\approx 1.320323632\ldots$

is the twin prime constant.

Skewes' number

Main article: Prime k-tuple § Skewes numbers

The Skewes' numbers for prime k-tuples are an extension of the definition of Skewes' number to prime k-tuples based on the first Hardy–Littlewood conjecture. The first prime p that violates the Hardy–Littlewood inequality for the k-tuple P, i.e., such that

$\pi _{P}(p)>C_{P}\operatorname {li} _{P}(p),$

(if such a prime exists) is the Skewes number for P.

Consequences

The conjecture has been shown to be inconsistent with the second Hardy–Littlewood conjecture.

Generalizations

The Bateman–Horn conjecture generalizes the first Hardy–Littlewood conjecture to polynomials of degree higher than 1.

References

• Aletheia-Zomlefer, Soren Laing; Fukshansky, Lenny; Garcia, Stephan Ramon (2020). "The Bateman–Horn conjecture: Heuristic, history, and applications". Expositiones Mathematicae. 38 (4): 430–479. doi:10.1016/j.exmath.2019.04.005. ISSN 0723-0869.
• Tóth, László (January 2019). "On the Asymptotic Density of Prime k-tuples and a Conjecture of Hardy and Littlewood". Computational Methods in Science and Technology. 25: 143–138. arXiv:1910.02636. doi:10.12921/cmst.2019.0000033.